波乗り道場FXmedia 
こんにちは！波乗り道場生のSioと申します。2021年12月に波乗り道場へ入門しました。
道場へ入門してからちょうど一年が経ち、2年生として新学期が始まったような気分です。
そしてありがたい事に波乗り道場のブログを担当させていただく事になりました。今回も最後までお付き合いの程、よろしくお願いいたします。
フィボナッチとは、レオナルド・フィボナッチと言う数学者が生み出した研究の成果だと私は思っております。
レオナルド・フィボナッチ氏は1170年頃にイタリアで生まれました。
彼は、数学や算術、代数学、幾何学などに興味を持ち、特にアラビア数学に深い関心を寄せていました。
当時、数学はヨーロッパではまだ発展途上の状態でしたが、アラビアで発展した数学の知識がイタリアやヨーロッパ全土に伝わりました。
レオナルド・フィボナッチ氏は、アラビアで発展した算術の知識を収集し、自身の著書『算盤の書』にまとめました。
この書物には、現在のフィボナッチ数列についての記述が含まれています。
そしてその『算術の書』にかの有名なウサギの繁殖に関する問題を取り上げフィボナッチ数列を明しています。
しかし実はこの数列・理論に名前が付いたのは彼が亡くなってからだいぶ経ってからです。
実際にフィボナッチ数列の名前が付けられたのは、19世紀になってからで、当時のフランスの数学者エドワード・ルーカス氏がフィボナッチ数列の研究をしており世の中に広めた一人といっても過言ではありません。
また学術界では彼がこのウサギの繁殖問題をフィボナッチ数列と名づけたとも言われております。
さてレオナルド・フィボナッチ氏の書かれた「算盤の書』で研究を進めた数列・理論とはどういったものだったのでしょう。
フィボナッチ数列は、前の2つの数を足し合わせてできる数列のことであり、1, 1, 2, 3, 5, 8, 13, 21, 34, …のように続いていく数列です。
この数列には、さまざまな法則がありますが、その中でも特に注目されるのが、隣り合う2つの数の比率が、黄金比と呼ばれる特別な数字に近づいていくという性質です。
そしてこの数列に導いてくれた問題がウサギの繁殖に関する問題でした。
フィボナッチがウサギの繁殖に関する問題を例に挙げたとされる話は、以下のような疑問でした。
ある牧場に、1組のウサギがいました。このウサギのペアは、生まれてから2か月で成熟し、その後、毎月1組の子ウサギを生むことができます。
ただし、生まれた子ウサギは、生まれてから2か月後に成熟し、また毎月1組の子ウサギを生むことができます。
この繁殖が始まってから1年後には、何組のウサギがいるか？
この問題を解くと、以下のようになります。
最初の月には1組のウサギがいるため、1組のウサギが生まれます。
2か月後には、この1組のウサギが成熟し、もう1組のウサギが生まれます。
つまり、2組のウサギがいます。
また、次の2か月後には、2組目のウサギが成熟して、新たに1組のウサギが生まれます。
この時点で、3組のウサギがいます。
つまり、最初の2項目は1,1であり、以降は前の2項目を足して得られるため、3項目は1+1=2、4項目は1+2=3、5項目は2+3=5というように続きます。
このように、フィボナッチ数列が誕生しました。
黄金比は、フィボナッチ数列から導き出すことができます。
まず、フィボナッチ数列を考えます。
この数列は、前の2つの数字を足した数が次の数になる数列であることを思い出してみましょう。
具体的には、最初の2つの数字が1,1であるとし、それ以降は前の2つの数字を足したものが次の数になるようにして数列を作ります。
隣り合う2つの数の比率を計算していくと、徐々に黄金比に近づいていくことがわかります。
例えば、最初の2つの数は1と1であり、その比率は1:1となります。次に、2番目の数と3番目の数の比率を求めると、2:1となります。
次に、3番目の数と4番目の数の比率を求めると、3:2となります。
このように、数列を進めていくことで、隣り合う2つの数の比率が、徐々に黄金比に近づいていくことがわかります。
この数列の中で、隣り合う2つの数字の比をとっていくと、次第に1.618…に近づいていきます。この数値が黄金比と呼ばれています。
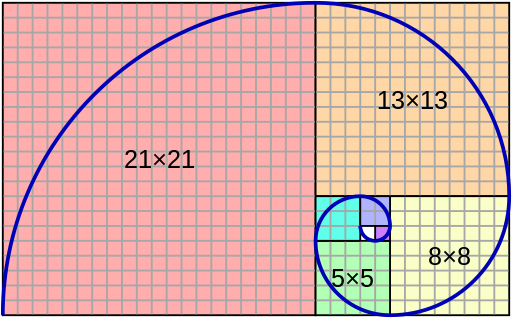
そしてこの黄金比の法則を表すのが1:1.618…の比率であり、自然界に多く見られる美しい比率となります。
たとえば、人間の身体比率や、葉っぱや貝殻の形状などにも現れています。
そしてこの黄金比を金融市場（FX）にて使った手法もたくさんあり多くのトレーダーはこれをテクニカル分析に使っています。
FXではチャート分析をする際にフィボナッチを引いて押しの強さであったり到達点を予測したりとすることもできます。
そして我々道場の師範であるジョニーさんは長年の経験と研究の末、もともとあるフィボナッチを相場に使うことから更なる次元へと考え方を深めていき、この波乗り道場で教えている波動論を作り上げられました。
具体的な波動の性質や波動論の説明は道場のYouTubeでジョニーさんが説明されていますのでぜひこちらの動画も併せて見てください。
フィボナッチとは元々はレオナルド・フィボナッチ氏が『算盤の書』に書いた自分の研究の一つでしたが、数百年の時を経今では色々な分野で使われている素晴らしい宇宙の法則だと感じております。
そして我が道場ではジョニーさんがこのフィボナッチの数列・理論を研究して今の波動論へと進化させました。
FXを勉強していく上で色々な手法や分析を学んでいくかと思います。
その中でも根本原理であるフィボナッチの数列や法則は必ず自分のトレードに役に立つと思います。
そして不思議なことに多くのものがこの数列から道びだされた数値に当てはまることから宇宙の法則と言っても過言ではないかと思います。
そしてこの数列から導き出される黄金比に沿ってFXも見ていくことによって新たな発見が見つかりました。
一見相場は自然が作り上げたものではないと思われるかと思いますが実は人間そのものも大きな宇宙という枠組みではこの法則の元生きているだけなのかもしれません。
宇宙の原理を知ることによって身近なところで活かすこともできると思います。
ぜひ波乗り道場で共にこの波動論を勉強して宇宙の法則であったり人生の深みも含めてトレードの勉強をしましょう。
